Barren Plateau Analysis
This notebook focuses on the analysis of the Barren Plateau problem. The code is heavily based on Tensorflow’s Quantum tutorial.
Install missing libraries
!pip install pandas seaborn matplotlib
Importing Libraries
# for simulation
import qandle
import torch
import qw_map
# for plotting
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# helper libraries
import random
import dataclasses
Setting up the problem
We use a fixed seed for reproducibility.
DEPTH = 50
NUM_REPEATS = 10
MAX_QUBITS = 5
qandle.config.DRAW_SHIFT_LEFT = True
qandle.config.DRAW_SHOW_VALUES = True
random.seed(42)
torch.random.manual_seed(42)
<torch._C.Generator at 0x29fc350dcf0>
Generate random circuits
Our circuits will first have a fixed layer, rotating each qubit by $R_y\left(\frac{\pi}{4}\right)$
pi8 = torch.tensor(torch.pi / 8)
# the matrix representation of the RY(pi/4) gate
ry_pi_4 = torch.tensor(
[[torch.cos(pi8), -torch.sin(pi8)], [torch.sin(pi8), torch.cos(pi8)]]
)
def generate_random_circuit(num_qubits, remapping=None):
layers = []
# initialize the circuit with RY(pi/4) gates on all qubits
for i in range(num_qubits):
layers.append(
qandle.CustomGate(
i, matrix=ry_pi_4, num_qubits=num_qubits, self_description="RY(pi/4)"
)
)
for _ in range(DEPTH):
for qubit in range(num_qubits):
# randomly choose a gate to apply
gate = random.choice([qandle.RX, qandle.RY, qandle.RZ])
layers.append(
gate(
qubit=qubit,
remapping=remapping,
)
)
# add CNOT gates, with even qubits as controls and odd qubits as targets
for control in range(0, num_qubits, 2):
target = control + 1
if target < num_qubits:
layers.append(qandle.CNOT(control=control, target=target))
# add CNOT gates, with odd qubits as controls and even qubits as targets
for control in range(1, num_qubits, 2):
target = control + 1
if target < num_qubits:
layers.append(qandle.CNOT(control=control, target=target))
# automatically split the circuit into smaller circuits if it is too large
return qandle.Circuit(layers, split_max_qubits=6)
Test a circuit
We generate a random circuit with 5 qubits and print it. We also execute it by calling example_circuit() and print the results.
example_circuit = generate_random_circuit(5)
print(example_circuit.draw())
print(example_circuit())
q0─RY(pi/4)_0─RZ_0 (0.88)─⬤─RX_0 (0.60)───⬤─RZ_0 (0.93)───⬤─RY_0 (0.43)───⬤─RX_0 (0.27)───⬤─RX_0 (0.27)───⬤─RY_0 (0.95)───⬤─RX_0 (0.81)───⬤─RY_0 (0.63)───⬤─RX_0 (0.28)───⬤─RZ_0 (0.01)───⬤─RZ_0 (0.71)───⬤─RY_0 (0.53)───⬤─RX_0 (0.40)───⬤─RX_0 (0.95)───⬤─RY_0 (0.11)───⬤─RX_0 (0.24)───⬤─RY_0 (0.38)───⬤─RZ_0 (0.61)───⬤─RX_0 (0.23)───⬤─RZ_0 (0.21)───⬤─RY_0 (0.16)───⬤─RY_0 (1.00)───⬤─RZ_0 (0.33)───⬤─RY_0 (0.50)───⬤─RX_0 (0.21)───⬤─RY_0 (0.93)───⬤─RY_0 (0.31)───⬤─RY_0 (0.69)───⬤─RZ_0 (0.60)───⬤─RX_0 (0.63)───⬤─RZ_0 (0.13)───⬤─RZ_0 (0.95)───⬤─RZ_0 (0.42)───⬤─RX_0 (0.25)───⬤─RY_0 (0.33)───⬤─RZ_0 (0.62)───⬤─RX_0 (0.76)───⬤─RZ_0 (0.41)───⬤─RX_0 (0.39)───⬤─RX_0 (0.05)───⬤─RZ_0 (0.20)───⬤─RX_0 (0.82)───⬤─RY_0 (0.98)───⬤─RZ_0 (0.18)───⬤─RY_0 (0.83)───⬤─RY_0 (0.09)───⬤─RX_0 (0.63)───⬤─RZ_0 (0.70)───⬤─RX_0 (0.15)───⬤───
q1─RY(pi/4)_1─RX_1 (0.92)─⊕─⬤─RX_1 (0.26)─⊕─⬤─RZ_1 (0.59)─⊕─⬤─RX_1 (0.89)─⊕─⬤─RZ_1 (0.44)─⊕─⬤─RZ_1 (0.36)─⊕─⬤─RX_1 (0.08)─⊕─⬤─RX_1 (0.58)─⊕─⬤─RX_1 (0.36)─⊕─⬤─RY_1 (0.79)─⊕─⬤─RY_1 (0.31)─⊕─⬤─RX_1 (0.66)─⊕─⬤─RZ_1 (0.16)─⊕─⬤─RZ_1 (0.91)─⊕─⬤─RY_1 (0.67)─⊕─⬤─RY_1 (0.16)─⊕─⬤─RY_1 (0.16)─⊕─⬤─RZ_1 (0.79)─⊕─⬤─RZ_1 (0.37)─⊕─⬤─RX_1 (0.96)─⊕─⬤─RZ_1 (0.62)─⊕─⬤─RX_1 (0.08)─⊕─⬤─RY_1 (0.59)─⊕─⬤─RY_1 (0.58)─⊕─⬤─RZ_1 (0.31)─⊕─⬤─RX_1 (0.33)─⊕─⬤─RZ_1 (0.66)─⊕─⬤─RY_1 (0.08)─⊕─⬤─RX_1 (0.09)─⊕─⬤─RX_1 (0.76)─⊕─⬤─RY_1 (0.28)─⊕─⬤─RY_1 (0.77)─⊕─⬤─RX_1 (0.61)─⊕─⬤─RY_1 (0.27)─⊕─⬤─RY_1 (0.48)─⊕─⬤─RZ_1 (0.13)─⊕─⬤─RY_1 (0.76)─⊕─⬤─RX_1 (0.69)─⊕─⬤─RX_1 (0.35)─⊕─⬤─RX_1 (0.51)─⊕─⬤─RX_1 (0.32)─⊕─⬤─RY_1 (0.19)─⊕─⬤─RZ_1 (0.73)─⊕─⬤─RZ_1 (0.57)─⊕─⬤─RZ_1 (0.86)─⊕─⬤─RY_1 (0.88)─⊕─⬤─RZ_1 (0.87)─⊕─⬤─RX_1 (0.50)─⊕─⬤─RX_1 (0.25)─⊕─⬤─RZ_1 (0.17)─⊕─⬤─
q2─RY(pi/4)_2─RX_2 (0.38)─⬤─⊕─RX_2 (0.79)─⬤─⊕─RZ_2 (0.87)─⬤─⊕─RX_2 (0.57)─⬤─⊕─RZ_2 (0.30)─⬤─⊕─RZ_2 (0.20)─⬤─⊕─RY_2 (0.89)─⬤─⊕─RZ_2 (0.90)─⬤─⊕─RX_2 (0.71)─⬤─⊕─RX_2 (0.59)─⬤─⊕─RX_2 (0.12)─⬤─⊕─RY_2 (0.49)─⬤─⊕─RZ_2 (0.65)─⬤─⊕─RX_2 (0.20)─⬤─⊕─RX_2 (0.98)─⬤─⊕─RY_2 (0.70)─⬤─⊕─RY_2 (0.77)─⬤─⊕─RZ_2 (0.11)─⬤─⊕─RX_2 (0.80)─⬤─⊕─RY_2 (0.33)─⬤─⊕─RZ_2 (0.43)─⬤─⊕─RX_2 (0.22)─⬤─⊕─RX_2 (0.65)─⬤─⊕─RX_2 (0.06)─⬤─⊕─RY_2 (0.47)─⬤─⊕─RZ_2 (0.11)─⬤─⊕─RZ_2 (0.08)─⬤─⊕─RX_2 (0.00)─⬤─⊕─RX_2 (0.87)─⬤─⊕─RZ_2 (0.90)─⬤─⊕─RY_2 (0.45)─⬤─⊕─RZ_2 (0.68)─⬤─⊕─RZ_2 (0.56)─⬤─⊕─RX_2 (0.93)─⬤─⊕─RX_2 (0.78)─⬤─⊕─RX_2 (0.68)─⬤─⊕─RZ_2 (0.59)─⬤─⊕─RY_2 (0.41)─⬤─⊕─RZ_2 (0.82)─⬤─⊕─RY_2 (0.47)─⬤─⊕─RZ_2 (0.92)─⬤─⊕─RX_2 (0.05)─⬤─⊕─RY_2 (0.06)─⬤─⊕─RZ_2 (0.37)─⬤─⊕─RZ_2 (0.27)─⬤─⊕─RZ_2 (0.68)─⬤─⊕─RY_2 (0.74)─⬤─⊕─RY_2 (0.12)─⬤─⊕─RZ_2 (0.40)─⬤─⊕─RZ_2 (0.67)─⬤─⊕─
q3─RY(pi/4)_3─RZ_3 (0.96)─⊕─⬤─RZ_3 (0.94)─⊕─⬤─RX_3 (0.57)─⊕─⬤─RX_3 (0.27)─⊕─⬤─RX_3 (0.83)─⊕─⬤─RZ_3 (0.55)─⊕─⬤─RZ_3 (0.58)─⊕─⬤─RY_3 (0.55)─⊕─⬤─RY_3 (0.95)─⊕─⬤─RY_3 (0.75)─⊕─⬤─RZ_3 (0.91)─⊕─⬤─RX_3 (0.89)─⊕─⬤─RY_3 (0.33)─⊕─⬤─RX_3 (0.20)─⊕─⬤─RX_3 (0.09)─⊕─⬤─RZ_3 (0.68)─⊕─⬤─RX_3 (0.30)─⊕─⬤─RZ_3 (0.25)─⊕─⬤─RZ_3 (0.84)─⊕─⬤─RY_3 (0.32)─⊕─⬤─RX_3 (0.14)─⊕─⬤─RX_3 (0.06)─⊕─⬤─RX_3 (0.03)─⊕─⬤─RZ_3 (0.28)─⊕─⬤─RX_3 (0.16)─⊕─⬤─RZ_3 (0.92)─⊕─⬤─RY_3 (0.85)─⊕─⬤─RX_3 (0.64)─⊕─⬤─RX_3 (0.13)─⊕─⬤─RY_3 (0.96)─⊕─⬤─RZ_3 (0.13)─⊕─⬤─RX_3 (0.66)─⊕─⬤─RZ_3 (0.06)─⊕─⬤─RY_3 (0.61)─⊕─⬤─RZ_3 (0.37)─⊕─⬤─RZ_3 (0.89)─⊕─⬤─RZ_3 (0.32)─⊕─⬤─RX_3 (0.37)─⊕─⬤─RY_3 (0.93)─⊕─⬤─RY_3 (0.62)─⊕─⬤─RX_3 (0.69)─⊕─⬤─RZ_3 (0.34)─⊕─⬤─RZ_3 (0.20)─⊕─⬤─RY_3 (0.71)─⊕─⬤─RX_3 (0.40)─⊕─⬤─RZ_3 (0.15)─⊕─⬤─RX_3 (0.92)─⊕─⬤─RX_3 (0.07)─⊕─⬤─RX_3 (0.21)─⊕─⬤─RX_3 (0.35)─⊕─⬤─
q4─RY(pi/4)_4─RY_4 (0.39)───⊕─RX_4 (0.13)───⊕─RZ_4 (0.74)───⊕─RX_4 (0.63)───⊕─RZ_4 (0.11)───⊕─RZ_4 (0.01)───⊕─RY_4 (0.34)───⊕─RY_4 (0.34)───⊕─RX_4 (0.79)───⊕─RY_4 (0.20)───⊕─RY_4 (0.64)───⊕─RZ_4 (0.14)───⊕─RZ_4 (0.65)───⊕─RZ_4 (0.20)───⊕─RX_4 (0.00)───⊕─RY_4 (0.92)───⊕─RZ_4 (0.80)───⊕─RX_4 (0.65)───⊕─RZ_4 (0.14)───⊕─RY_4 (0.02)───⊕─RZ_4 (0.51)───⊕─RY_4 (0.18)───⊕─RZ_4 (0.17)───⊕─RY_4 (0.20)───⊕─RY_4 (0.16)───⊕─RZ_4 (0.40)───⊕─RZ_4 (0.36)───⊕─RZ_4 (0.39)───⊕─RX_4 (0.41)───⊕─RZ_4 (0.10)───⊕─RY_4 (0.96)───⊕─RZ_4 (0.23)───⊕─RY_4 (0.71)───⊕─RY_4 (0.22)───⊕─RZ_4 (0.21)───⊕─RX_4 (0.03)───⊕─RZ_4 (0.76)───⊕─RZ_4 (0.55)───⊕─RY_4 (0.45)───⊕─RX_4 (0.64)───⊕─RX_4 (0.48)───⊕─RX_4 (0.67)───⊕─RX_4 (0.42)───⊕─RX_4 (0.31)───⊕─RZ_4 (0.00)───⊕─RY_4 (0.01)───⊕─RX_4 (0.76)───⊕─RZ_4 (0.03)───⊕─RX_4 (0.41)───⊕─RX_4 (0.81)───⊕─
tensor([-0.0467-0.0167j, 0.0193+0.0381j, -0.0579+0.0531j, -0.1009+0.0247j,
-0.0376-0.0387j, 0.1489-0.2305j, 0.1670+0.1326j, 0.1559-0.0838j,
-0.0400+0.1098j, 0.0273-0.0980j, 0.1197+0.0842j, 0.0106+0.0614j,
-0.0582-0.0663j, 0.1070+0.0359j, -0.1660+0.0154j, 0.0214+0.2573j,
0.2015+0.0565j, 0.1741+0.0247j, 0.1957-0.1046j, 0.1736-0.0766j,
-0.1005+0.0296j, -0.1508+0.2421j, 0.2027+0.1465j, -0.1216+0.3213j,
0.0887-0.1136j, -0.1085+0.0037j, 0.0871-0.0682j, 0.0768+0.1639j,
-0.0379+0.2979j, 0.0689+0.1266j, -0.0245-0.1873j, 0.0356-0.0349j],
grad_fn=<SqueezeBackward4>)
Measure the gradients
We create NUM_REPEATS random circuits, and measure their gradients after a forward and backward pass. The mean and standard deviation of the gradients are saved in a pandas DataFrame.
@dataclasses.dataclass
class GradData:
"""Helper class for neatly storing gradient data before converting to a DataFrame."""
num_qubits: int
remapping: str
grad_std: float
grad_mean: float
circ_grads = []
combinations = [[r, q] for r in [None, qw_map.tanh] for q in range(2, MAX_QUBITS + 1)]
for remapping, num_qubits in combinations:
remap_str = remapping.__name__ if remapping is not None else "None"
for _ in range(NUM_REPEATS):
c = generate_random_circuit(num_qubits, remapping=remapping)
# forward pass and backward pass using a dummy loss
c().sum().abs().backward()
c_grads = [p.grad.item() for p in c.parameters() if p.grad is not None]
c_grads = torch.tensor(c_grads)
# standard deviation of the gradients
grad_std = c_grads.std().item()
# we use the absolute value of the mean gradient
grad_mean = c_grads.abs().mean().item()
circ_grads.append(GradData(num_qubits, remap_str, grad_std, grad_mean))
df = pd.DataFrame([dataclasses.asdict(gd) for gd in circ_grads])
Plot the results
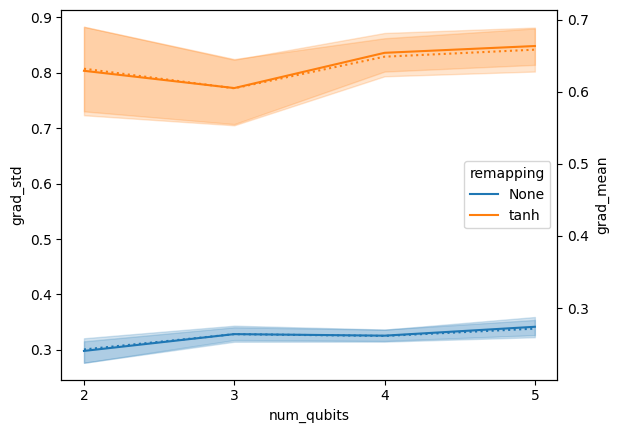
Remapping increases both mean absolute gradient and standard deviation.
fig, ax = plt.subplots()
pltargs = dict(data=df, x="num_qubits", hue="remapping")
sns.lineplot(**pltargs, ax=ax, y="grad_std", linestyle="-")
sns.lineplot(**pltargs, ax=ax.twinx(), y="grad_mean", linestyle=":", legend=False)
# set major x ticks to integer values
ax.xaxis.set_major_locator(plt.MaxNLocator(integer=True))